강화학습 1강. Q-Learning
* "혁펜하임"님의 유튜브 강의를 보고 주로 공부하고 이해한 게시물입니다. 추가적으로 참고한 곳은 링크를 걸어두었습니다. 좋은 정보 제공 감사합니다!
Q-Learning이란?
- 강화학습의 Model-Free 알고리즘 중 하나
(강화학습 알고리즘에는 Model-Free, Model-Based 알고리즘이 있다. 자세한 내용은 https://spinningup.openai.com/en/latest/spinningup/rl_intro2.html)
Q-Learning 은 아래와 같은 격자에서 맵을 모른채로 목적지(Ending Point)를 찾아가는 것과 같습니다.

어떻게 이동할까?
Greedy Action 으로 이동할 것입니다. Greedy 로 이동한다는 것은 매번 이동하면서 이동에 대한 점수를 매기고, 점수가 큰 쪽으로 이동할 것을 의미합니다. 위의 격자같은 경우는 각 위치(state)에서 상,하,좌,우 로 4가지 이동(action)을 할 수 있으므로, 각 위치(state)마다 4개의 점수를 가지고 있을 것입니다.
처음에는 아무런 정보가 없기 때문에 출발점에서 무작위로 이동할 것입니다. 그러다 우연히 목적지(Ending Point)에 도달하게 되면, 다음 시행을 위해 직전의 위치(state)와 이동(action)에 대해 점수를 줌으로써 정보를 남겨놓는 것입니다. 이때 점수를 보상, Reward라고 합니다.

- 각 칸의 X 표시 기준으로 상,하,좌,우는 해당 위치(state)의 상,하,좌,우 이동(action)에 대한 점수를 의미
- 처음에 점수는 모두 0으로 시작하며, 위 위치에서는 "상"으로 이동했을 때 보상 Reward를 받은 경험이 있기 때문에 1로 업데이트.
이때, 각 위치(state)에서 이동(action)에 대한 점수를 Q-value 라고 합니다. Q-value 의 "Q" 는 Quality의 Q이며, 각 위치에서 이동(action)의 가치를 의미합니다. 즉, 여기서 Action 에 대한 가치는 이 Action을 취했을 때, 앞으로 받을 보상으로 평가한다고 볼 수 있습니다. (https://mangkyu.tistory.com/61)
위에서 Ending Point에 도달한 이후, 다시 Ending Point를 찾아가는 시행을 할 것입니다. 이때, 모든 state의 Q-value가 아직은 0일 것이기 때문에 무작위로 움직일 것입니다. 그러다가 이전 시행에서 Ending Point 직전에 있던 위치(state)에 우연히 도달하게 됩니다. 그러면, 다시 직전 state와 action에 대해 평가하는 Q-value를 업데이트합니다. (사실은 이전에도 모든 이동마다 Q-value를 업데이트 합니다.) 이때, Ending Point 아래 위치에 도착하므로써 직접적으로 보상을 받지는 않지만, 그 다음에 보상을 받을 걸로 기대되어 해당 위치의 Action 중 가장 큰 Q-value인 1로 업데이트 시켜줍니다.

이러한 시행을 반복하며 모든 state와 action에 대해 계속 평가합니다. 그러면서 자동으로 적절한 Q-value를 찾아갑니다.
Exploration (탐험)
위와 같이 보상이 높은 쪽으로만 이동하는 시행을 반복하면, Ending Point를 찾아갈 수는 있지만, 처음에 찾은 경로로만 가게 됩니다. 만약 아래와 같이 처음에 목적지를 찾았다면, 다른 곳은 가보지도 않고, 계속해서 저 경로로만 이동해서 목적지를 찾아갈 것입니다. 더 좋은 경로가 있을지도 모르는데요.

그래서 가보지 않은 길을 가는 Exploration(탐험)이 필요합니다. Exploration 을 실행하기 위해서 ε-Greedy 를 수행합니다. ε-Greedy란, 항상 높은 Q-value 값의 이동만 하는 것이 아니라 ε의 확률만큼은 Random하게 움직이는 것을 말합니다.
ε-Greedy를 이용하여 Exploration을 하면, 목적지로 가는 새로운 경로를 찾을 수도 있을 뿐만 아니라, 새로운 목적지를 발견할 수도 있습니다. 목적지가 하나인데 이게 웬 말인가 싶을 수도 있겠지만, 실제 상황에서는 Ending Point 를 알고 있지도 않으며, Map을 모른 채로 학습합니다. Ending Point가 하나로 정해져 있지도 않습니다. 예를 들어, 바둑에서 여러 전략이 존재하듯이 여러 방법이 있고, 더 좋은 전략이 있을 수도 있습니다.
ε을 높게 설정할 수록 새로운 길을 많이 탐험하며, ε을 작게 설정할수록 기존에 알고 있는 방법을 고수합니다. 그래서, 처음에는 많은 시도를 하도록 ε을 높게 설정하고, 많은 시행할수록 탐험을 줄이도록 ε을 줄여나가는 Decaying ε-Greedy 방법을 많이 씁니다. 예) ε : 0.9→0
더 효율적인 방법
Exploration을 통해 아래 그림에서 2번 경로를 새롭게 알게되었다고 합시다. 2번 경로가 더 효율적이기 때문에 2번 경로를 선택하는 게 더 합리적으로 보이지만, 지금까지의 Q-Learning에 의하면, 2번경로와 1번경로 모두 같은 확률로 이동하게 될 것입니다.

그래서 도입하는 것이 Discount factor(할인율)입니다. Discount factor를 적용함으로써 보상을 받을 수 있는 시점에 따라 차별을 두게 됩니다. 더 먼 미래의 보상일수록 Discount factor, γ (0<γ<1)를 많이 곱해주어 가치를 삭감합니다.
그러면 가까운 미래에 보상을 받는 Action이 더 높은 Q-value를 가지게 될 것이고, 더 가까운 경로로 이동하게될 가능성이 높아집니다. 이는 더 효율적인 방법을 추구할 수 있게 만듭니다.
Discount factor를 Q-value에 반영하는 방법은 업데이트할 때 이뤄집니다. Action 후 업데이트 하는 과정에서 다음 state의 가장 큰 Q-value를 가져올 것입니다. 그때, 바로 가져오는 것이 아니라, γ를 곱해준 뒤에 가져옵니다. 그러면 매단계마다 γ를 곱해주어 보상을 받을 시점까지 남은 단계만큼 γ를 곱해주는 꼴이 됩니다. 그만큼 Q-value는 작아질 것이고요 (γ는 0과 1사이의 값이기 때문에).
처음부터 이 과정을 반복하여 Q-value를 업데이트 했다면, 아래와 같은 값들을 가지게 될 것입니다. 아래와 같은 환경이라면, 4행1열 위치에 도달하게 되면 더 높은 Q-value (γ2>γ4)를 가진 "오른쪽"으로 이동하여 2번경로를 선택할 확률이 높아집니다. 1번 경로와 2번 경로에 차별이 없었는데, 효율성으로 차별을 두게 된 것입니다.

γ가 작을수록, 시간의 흐름에 따른 가치 훼손을 크게 반영합니다. γ가 클수록, 시간의 흐름에 따른 가치 훼손을 적게 반영하구요.
Q-Update
지금까지 보았듯, Q-value는 state(위치)에서 action(행동)의 가치를 나타냅니다. 이 Q-value를 업데이트 하는 것은 지금까지처럼 숫자를 바꿔치기 하듯이 이뤄지지 않습니다. 점차 부드럽게 update 해나갑니다. 수식으로 보면 아래와 같습니다. (수식 참고: https://mangkyu.tistory.com/61)
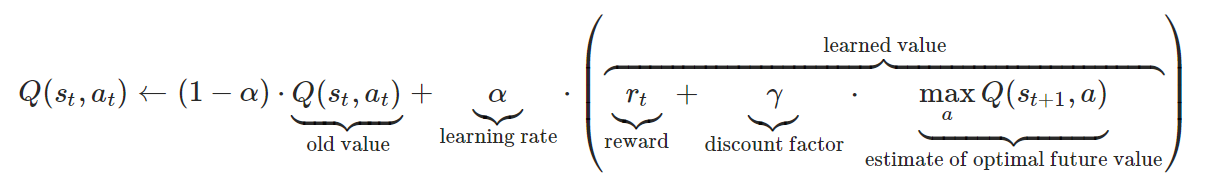
Q-value는 행동 가치 함수라는 Q 함수로 표현되어 있고,
점차 부드럽게 업데이트 해나갈 수 있도록 학습률, α가 사용되었습니다.
reward는 action(행동) 직후 보상을 받을 경우 (목적지에 도착했을 때), 그 보상을 의미합니다. 이때는 Discount factor를 곱하지 않습니다.
discount factor 는 action(행동) 직후 즉각 보상을 받는 경우가 아닐 때, 다음 state에서 max Q-value를 반영시키기 전에 γ를 곱해주는 과정입니다.
estimate of optimal future value 는 action 직후 다음 state의 action 중 가장 큰 Q-value를 의미합니다.
